It sometimes happens that the obvious is long disregarded, and this applies to the first principle of comminution. Over the years many careful laboratory investigations of comminution phenomena have been made and published. These included accurate measurements of energy input and product size particle distributions, but the results differed among themselves and have not been conclusive. In practically every case the energy level of the feed particles was ignored, and considered to be zero.
Since any separation of matter requires the application of energy, it follows that the existence of any particles of finite size registers a prior energy input. The energy register is defined, here as the total specific energy input, or total energy input per unit of mass, experienced in effective particle separation. All particulate matter thus has a positive energy register, whose value increases as the particle size decreases. The energy register corresponds to the level of the energy input effective in comminution, or to the cumulative specific energy required in the formation of all particles below infinite size. It does not correspond to the energy content, since nearly all of the energy input required has been transformed into heat and removed, after registering as particle size reduction. The energy register maybe said to correspond to the total specific energy experienced by the particulate material or to its energy input history.
The first principle states that comminution calculations should be based upon the energy register of the feed and product, and that in any instance the specific energy input equals the energy register of the product minus the energy register of the feed. According to the first principle, all comminution calculations should refer to the same particle size base, that of infinity, rather than to the arbitrarily selected size base of any feed sample.
The effects of selecting diverse feed sizes as the finite base size is illustrated in Table I and Figure 1. A hypothetical ore is crushed to a size of 15,000 microns, ground wet in a rod mill to 1000 microns, and then ground wet in a ball mill to the various micron sizes of 300, 250, 200, and 100. In this example the product size represents the size in microns which 80% of the product passes. The total specific energy input in Kwh per short ton, or the energy register, required to produce each product size, is listed in Col. (A) of Table I. Col. (B) lists the energy input required per ton of rod mill feed, and Col. (C ) lists the energy required, per ton of ball mill feed.
It is seen from Fig. 1 that the energy register in Col. (A) plots as a straight line with a slope of 1:2. Col. (C) forms a curved line with the approximate slope of 1:1 and Col. (B) forms a slightly curved line of intermediate slope.
It is evident that the selection, of an energy base size can be very important in predicting crushing and grinding results. For example, line (A) in Fig. 1 shows that 14.5-4.00, or 10.5 Kwh/ton would be required to grind from 900 to 70 microns, while line (C) would indicate that 12.9-1.02, or 11.88 Kwh/ton would be necessary. If the first principle is accepted the energy register line (A) with the base size of infinity is correct for predicting the energy input required from any feed size to any product size, and the other straight lines with finite base sizes give distorted results. As the finite energy base size is increased, the calculated energy input required for any feed and product size approaches that required according to the first principle with its infinite energy base size. The slope of the log-log plot of energy input versus product size varies with the energy base size selected, and according to the first principle, it is correct for all particle sizes only when the energy base size is infinity.

The second principle defines the regular relationship between the energy input and the feed and product sizes when the energy base size is infinity according to the first principle. It makes the theoretical and practical solution of comminution problems possible.
Since comminution depends primarily upon the development of flaws into crack tips, and since the extension of a crack tip into, a break is accomplished by the concentration of energy at the crack tip which was already resident in the particle as strain energy, it follows that the energy input necessary for breakage is proportional to the transverse length of the crack tips formed. The crack length per unit volume of solid material, or the specific crack length Cr, in centimeters per cubic centimeter of solid, is inversely proportional to the square root of the diameter of regular and similar particles. If d is the particle diameter in microns, and if the ratio between surface area and particle volume is the same as that of cubes, then the crack length Cr is √30,000/d. cm. per cc, and the surface area is 60,000/d. sq. cm. per cc.
The second principle states that the energy input is directly proportional to the new crack length produced. According to the first and second principles the energy input is regularly proportional to one over the square root of the product particle diameter minus one over the square root of the feed particle diameter.
If f represents the feed particle diameter and p the product particle diameter, then
Energy Input = K/√p – K/√f…………………………………………………………..(1)
where K is a proportionality constant. The first term on the right hand side of Eq. (1) represents the energy register of the product, the last term represents the energy register of the feed, their difference is the energy input according to the first principle, and the square root signs result from the second principle.
The Third, or Bond,, theory of comminution was named, to distinguish it chronologically from the first (Rittinger) and second (Kick) theories. It was based upon the first and second principles, although these were not formally stated when, the theory was presented in 1951. Certain conventional units were used to make it directly applicable to commercial crushing and grinding problems.
The sizes in microns of the square openings which 80% of the complete crushed or ground material would pass were selected as the practical criteria of the feed and product sizes. These are designated as F and P. If fines have been removed from the feed F must be increased to the size Fc which has an equivalent energy register. The energy input W is expressed as kilowatt-hours per short ton, and the work index Wi is the energy register in Kwh/ton of a product with 80% passing 100 microns, equivalent to about 67% passing 200 mesh. The work input in joules, or watt-seconds, per gram is 3.97 W.
The work index equation, which in various forms is used in the solution of nearly all crushing and grinding problems, is
W = 10 Wi/√P – 10 Wi/√F………………………………………………………………………(2)
Wi corresponds to the proportionality constant K in Eq. (1) and 10 is the square root of the 100 micron size. The energy register of the product is 10Wi/√P and that of the feed is 10 Wi/√F. In Table I the work index value is 12.0.
Eq. (2) contains four different quantities.; When any three of these are known the other can be found by transposing the equation. Useful forms are:

In agreement with the first and second principles, the work index Wi of any material with homogeneous breakage remains constant over all size ranges of crushing and grinding. However, it frequently happens that the work index is found to increase or decrease as the product size becomes smaller. This can result when:
(a) The material contains natural grain sizes, as in sandstone, with a marked deficiency of material in the size range immediately above the natural grain size and an excess below. In such cases the Wi value is low at coarse sizes, increases rapidly as the natural grain size is approached, and ordinarily decreases at finer sizes
(b) The material contains-incipient cracks or laminations, which have much the same effect as natural -grain sizes but in a coarser size range.
(c) In fine dry grinding the work index increases because of cushioning caused by the fine particles present, and much the same effect has been observed in wet grinding. In the finer micron sizes the increase may be augmented by approach to the grind limit size of 0.1 micron. When the 80% passing size P is less than 70 microns the work index is multiplied by the following empirical factor:
P + 10.3/1.145 P
(d) The reduction apparatus may be less efficient at one size range than at another, resulting in an increased work index. For instance, the grinding,balls may be too large or too small for the feed size.
This response of the work index to changes in physical properties of the material, and in grinding conditions, makes it a valuable practical criterion for commercial crushing and grinding. The work index can be found in any plant operation where the energy input and feed and product sizes are known. Comparison of the Wi values from different operations in the same plant, from different plants, and from laboratory crushing and grinding tests on the same material, can be of considerable value in increasing size reduction efficiency and in selecting equipment for new operations.
Brittle materials are commonly not homogeneous, but contain internal zones of weakness, laminations, mineral grain boundaries incipient cracks, and planes of molecular displacement between the regular space lattices. In addition, irregularly broken pieces contain re-entrant angles and other surface configurations which develop into surface cracks under strain. All of these conditions are collectively called flaws; a flaw being defined as any location which is weaker than its surroundings and tends to develop into an external or internal crack tip when the particle is placed under strain.
Rock breakage is controlled by the distribution and magnitude of its contained flaws. The weakest flaw determines the first break, and affects the number of additional breaks developed, from one straining operation. Consequently, the number of progeny particle s produced from one progenitor depends upon the relative strength of the different flaws which develop into cracks. If a rock contains one very weak flaw it breaks easily into two pieces; if it contains a considerable number of stronger flaws it will require more work input to cause breakage, but breakage will produce many progeny particles. The work index may remain the same in both cases.
If a completely homogeneous one-inch cube of brittle rock can be imagined under equally distributed compression on two parallel opposite sides, it will require a very large work input to break, and will finally fall explosively to produce an immense progeny of fine dust particles. However, it s work index may be no higher than that required to break a similar cube with a weak flaw into a few pieces.
Tests on the breakage of successive rock pieces of similar material, size and shape, usually show a surprising range of work input required, with an inverse proportion between the breaking strength and the square root of the particle diameters produced, resulting in a fairly constant work index.
From the comminution standpoint a completely homogeneous material contains no flaws larger than the grind limit of about 0.1 micron. No naturally occurring completely homogeneous brittle materials are known.
A material of homogeneous breakage has a constant work index at different size ranges. Its flaws can vary, greatly in breaking strength and in distribution in different specimens, but they are not concentrated at any size range.
A material of heterogeneous breakage has an uneven flaw distribution which is concentrated at certain size ranges. An example is loosely cemented sandstone with a natural grain size. The work index of such materials varies at different product sizes. It increases as the decreasing product size approaches the natural grain size, or the size of greatest flaw concentration, and it decreases below that size.
The breakage of a single particle of diameter d microns under one straining operation results in the formation of a progeny of product particles of different sizes. The reduction ratio rr of the single break can be obtained by dividing the equivalent value Fc of the feed particle from Table II by the 80% passing size P in microns of the product progeny. The energy input required to break can be taken as the breaking strength multiplied by one-half of the measured deflection at breakage. The work index of the single break can be calculated by Eq. (3) from the energy input required, reduced to W Kwh/ton, and the values of P and Fc.
The Third Principle states that work index variations in the grinding of a material to different product sizes denote heterogeneous breakage, and are the result of a concentration of its flaw structure at one or more particle size ranges. The work index continues constant for feed, particles of homogeneous breakage, even though their product sizes, reduction ratios, and work input requirements may differ widely.

The energy register is the total specific energy input above the breakage threshold to a comminution feed or product. It includes the large amount of energy input effective in breakage which has been dissipated as heat. It is expressed, in kilo-watt-hours per short ton required for reduction from theoretically infinite feed size. The Third Theory work index Wi is the energy register to 80% passing 100 microns.

The first principle of comminution states that the specific energy input always equals the energy register of the product minus the energy register of the feed;. Disregard, of this principle and assignment of zero energy register to the feed, results in a distorted, interpretation of comminution results. This distortion Increases as the feed size decreases.
The second principle states that the useful work input is directly proportional to the new crack length produced in breakage, and therefore it is inversely proportional to the square roots of the particle sizes. The Third Theory of Comminution results from the first and second principles in combination.
The Third, principle deals with the distribution of flaws in comminution feed; and the effect on breakage. It shows that the concentration of flaws in certain size ranges is characteristic of materials of heterogeneous breakage, and explains variations in the work index values when reducing such materials to different product sizes.
New equations derived in 1960 for calculating the work index values from ball mill and rod mill grindability tests are given, and new exponential size distribution equations are included.
Empirical corrections for use in the work index equation are given for scalped or sized feed, not containing its natural quota of fines. Some particle count, or progeny, equations are included.

Finding the best circuit to crush and grind minerals to beneficiation sizes is a complex problem that can lead to interminable discussion. Conclusions reached can be questioned. This will continue as long as the technology of comminution continues to expand, and is a mixture of many technical and economic factors in what is not a precise science.
Laboratory and pilot plant procedures now exist that can help process engineers make sound decisions on which circuits are the best for crushing and grinding the specific ore being studied. It is the aim of this paper to discuss such procedures so a better understanding of key decision parameters is available to the profession, and to update comminution testing which has seen a period of change in which new procedures have been introduced.
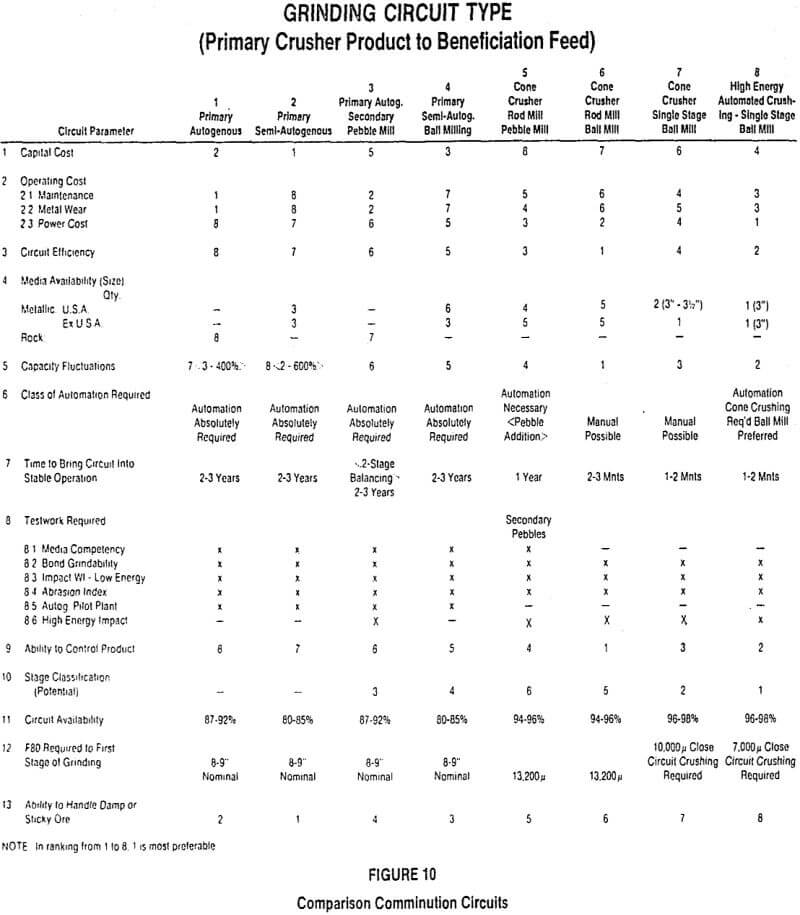
On Figure 10, one category is named “Required Testing”. This lists the tests necessary to design the comminution circuit and to select the equipment needed in the circuit. Initial bench scale comminution tests should be run to establish some or all of the following physical characteristics of the ore that are related to how the ore can be crushed and ground:
The testwork can be broken down into two categories:
